Terence Tao is a Fields' medalist. "
Timothy Gowers remarked on Tao's accomplishments:
[12]
Tao's mathematical knowledge has an extraordinary combination of breadth and depth: he can write confidently and authoritatively on topics as diverse as partial differential equations, analytic number theory, the geometry of 3-manifolds, nonstandard analysis, group theory, model theory, quantum mechanics, probability, ergodic theory, combinatorics, harmonic analysis, image processing, functional analysis, and many others. Some of these are areas to which he has made fundamental contributions. Others are areas that he appears to understand at the deep intuitive level of an expert despite officially not working in those areas. How he does all this, as well as writing papers and books at a prodigious rate, is a complete mystery. It has been said that Hilbert was the last person to know all of mathematics, but it is not easy to find gaps in Tao's knowledge, and if you do then you may well find that the gaps have been filled a year later." [Source Wikipedia]
Therefore I was happy to find that he wrote on
his blog dimensional analysis (and, implicitly about the
Pi Theorem).
Here below I am getting verbatim the introduction of his blogpost:
"Mathematicians study a variety of different mathematical structures, but perhaps the structures that are most commonly associated with mathematics are the number systems, such as the integers
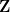
or the real numbers
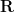
. Indeed, the use of number systems is so closely identified with the practice of mathematics that one sometimes forgets that it is possible to do mathematics without explicit reference to any concept of number. For instance, the ancient Greeks were able to prove many theorems in Euclidean geometry, well before the development of
Cartesian coordinates and
analytic geometry in the seventeenth century, or the formal constructions or axiomatisations of the real number system that emerged in the nineteenth century (not to mention precursor concepts such as zero or negative numbers, whose very existence was highly controversial, if entertained at all, to the ancient Greeks). To do this, the Greeks used geometric operations as substitutes for the arithmetic operations that would be more familiar to modern mathematicians. For instance, concatenation of line segments or planar regions serves as a substitute for addition; the operation of forming a rectangle out of two line segments would serve as a substitute for multiplication; the concept of similarity can be used as a substitute for ratios or division; and so forth.
A similar situation exists in modern physics. Physical quantities such as length, mass, momentum, charge, and so forth are routinely measured and manipulated using the real number system
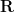
(or related systems, such as
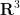
if one wishes to measure a vector-valued physical quantity such as velocity). Much as analytic geometry allows one to use the laws of algebra and trigonometry to calculate and prove theorems in geometry, the identification of physical quantities with numbers allows one to express physical laws and relationships (such as Einstein’s famous mass-energy equivalence
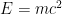
) as algebraic (or differential) equations, which can then be solved and otherwise manipulated through the extensive mathematical toolbox that has been developed over the centuries to deal with such equations.
However, as any student of physics is aware, most physical quantities are not represented purely by one or more numbers, but instead by a combination of a number and some sort of unit. For instance, it would be a category error to assert that the length of some object was a number such as
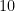
; instead, one has to say something like “the length of this object is
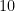
yards”, combining both a number
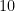
and a unit (in this case, the yard). Changing the unit leads to a change in the numerical value assigned to this physical quantity, even though no physical change to the object being measured has occurred. For instance, if one decides to use feet as the unit of length instead of yards, then the length of the object is now
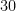
feet; if one instead uses metres, the length is now

metres; and so forth. But nothing physical has changed when performing this change of units, and these lengths are considered all equal to each other:
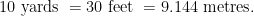
It is then common to declare that while physical quantities and units are not, strictly speaking, numbers, they should be manipulated using the laws of algebra as if they were numerical quantities. For instance, if an object travels
metres in
seconds, then its speed should be

where we use the usual abbreviations of
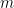
and

for metres and seconds respectively. Similarly, if the speed of light

is
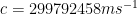
and an object has mass
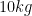
, then Einstein’s mass-energy equivalence
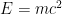
then tells us that the energy-content of this object is

Note that the symbols
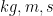
are being manipulated algebraically as if they were mathematical variables such as

and
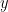
. By collecting all these units together, we see that every physical quantity gets assigned a unit of a certain dimension: for instance, we see here that the energy
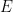
of an object can be given the unit of
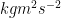
(more commonly known as a
Joule), which has the dimension of
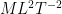
where
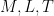
are the dimensions of mass, length, and time respectively.
There is however one important limitation to the ability to manipulate “dimensionful” quantities as if they were numbers: one is not supposed to add, subtract, or compare two physical quantities if they have different dimensions, although it is acceptable to multiply or divide two such quantities. For instance, if
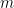
is a mass (having the units
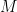
) and

is a speed (having the units
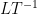
), then it is physically “legitimate” to form an expression such as
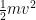
, but not an expression such as
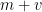
or
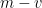
; in a similar spirit, statements such as

or
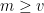
are physically meaningless. This combines well with the mathematical distinction between vector, scalar, and matrix quantities, which among other things prohibits one from adding together two such quantities if their vector or matrix type are different (e.g. one cannot add a scalar to a vector, or a vector to a matrix), and also places limitations on when two such quantities can be multiplied together. A related limitation, which is not always made explicit in physics texts, is that transcendental mathematical functions such as
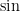
or
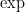
should only be applied to arguments that are dimensionless; thus, for instance, if

is a speed, then

is not physically meaningful, but
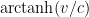
is (this particular quantity is known as the
rapidity associated to this speed).
These limitations may seem like a weakness in the mathematical modeling of physical quantities; one may think that one could get a more “powerful” mathematical framework if one were allowed to perform dimensionally inconsistent operations, such as add together a mass and a velocity, add together a vector and a scalar, exponentiate a length, etc. Certainly there is some precedent for this in mathematics; for instance, the formalism of
Clifford algebras does in fact allow one to (among other things) add vectors with scalars, and in differential geometry it is quite common to formally apply transcendental functions (such as the exponential function) to a differential form (for instance, the
Liouville measure 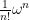
of a symplectic manifold can be usefully thought of as a component of the exponential
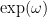
of the symplectic form
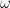
).
However, there are several reasons why it is advantageous to retain the limitation to only perform dimensionally consistent operations. One is that of error correction: one can often catch (and correct for) errors in one’s calculations by discovering a dimensional inconsistency, and tracing it back to the first step where it occurs. Also, by performing
dimensional analysis, one can often identify the form of a physical law before one has fully derived it. For instance, if one postulates the existence of a mass-energy relationship involving only the mass of an object
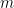
, the energy content
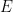
, and the speed of light

, dimensional analysis is already sufficient to deduce that the relationship must be of the form
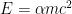
for some dimensionless absolute constant
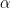
; the only remaining task is then to work out the constant of proportionality
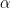
, which requires physical arguments beyond that provided by dimensional analysis. (This is a simple instance of a more general application of dimensional analysis known as the
Buckingham  theorem
theorem.) [
Continue reading on Tao's blog]





