Data over Space and Time course by Cosma Shalizi

I confess I am a fan of Cosma Shalizi (GS). I do not know him, I do not know if he is a nice person or bad ass. He dos not know me. For sure I like the way he approaches statistics and his book (under the previous link). I am also astonished by his blog and the flood and variety of his readings.  Now he is giving a class on Spatial and temporal statistic. Topics that I think are necessary to know by Hydrologists. His class can be found here.

I hope that he does not mind if I cross reference his material.

Controllability and Dynamical Systems

Wow! There is a lot of literature on dynamical systems. Originally, when i though to dynamical systems I identify them with the non linear dynamical systems which produced chaos (e.g. Strogatz, 1994) or to elegant geometric representations of mechanics (Arnold, 1983, 1989 ). Looking to lumped hydrological models as dynamical systems opened to me new perspectives. The more important one: learning dynamical systems from system dynamics. Said this way, it seems a joke or a tautology. However system dynamics is its own discipline. It can be think to originate from von Bertalanffy but it is conjugate as “System and Control” since Kalman (e.g. Kalman, 1968). Wilems (e.g. Polderman and Wilems, 1998) offers a little different (but interesting) perspective (and a terrible notation).

 
When one think to a systems of ordinary differential equations (ODEs), obviously the thoughts go to their solutions. Does exist a solution for such a system ? Is it unique ? A mantra that we learned since our first courses on calculus. However “System and Controls” steers towards different concepts (e.g. Luenberger, 1979 or Kalilath, 1980 or more mathematically, Sontag, 1998). In fact the concept of control implies to study the conditions under which the ODEs systems solution can be moved to a precise beahvior (Willems, 2007) by actuators, i.e., external inputs (fluxes ?) to the state variables. This condition was easily translated into the determination of the rank of a special matrix, first written by Kalman (e.g. Liu and Barabási, 2016). Other equivalent formulation include the Gramian integral. What exactly means this property said “controllability” ? It means no more that what is intended: that trough a number of external actions you can move the systems to any conceivable state. Let $x_1$ to $x_n$ these variables, then you have to be sure that that all the n-dimensional vector domain can be spanned under the action of actuators, and the Kalman result, just establish the condition under which this is possible. I did not mention however, that the above results are valid for linear systems: a great result but a little poor in scope, since most of the problem we have are nonlinear. Fortunately people piooneered studies on the controllability on non linear systems since the seventies (Heines and Hemes, 1970; Hermann and Kremer, 1977; Cornelius et al, 2013, Isidori, A., 2013).
The application field of controllability had its first application oh hydraulic and mechanical engineering (e.g. Polderman and Wilems, 1998) , but soon moved to other systems. Notably: ecology (Iglesias and Ingals, 2010), brain (Lynn and Basset, 2018) , internet connections ( Liu and Barabási, 2016). There is then hope that those studies also impact hydrological and earth system sciences.
I did not mentioned it but really entangled with the more recents developments of the matter, there is the study of graph theorethic methods applied to the dynamical system (Yamada and Fouls,1990). Barabasi and Liu (Liu and Barabási, 2016) wrote a recent review that practically starts from the illustration of the systems with graph.
Made the note that I believe that Petri Nets are more exppressive than those used by Barabasi, I found the graph methods more easy to grasp and intuitive. Possibly one can also see connections between the results here (in dynamical systems) and some of those in causality theory (Pearl et al., 2016). For instance the theorem regarding the structural controllability of systems described by graphs (see in Lu and Barabási, 2016) recall the theorems on correlations in causality theory. A system which is correlated, read as a causal graph, is not controllable (it seems). A-posteriori, this seems obvious, since correlation, means some type of limitation on the phase space explorability.


References

• Arnold, V. L. (1983). Geometrical methods in the theory of ordinary differential equations. Springer-Verlag. 
• Arnold, V. L. (1989). Mathematical Methods of Classical Mechanics 2nd ed, 1–536. 
• Cornelius, S. P., Kath, W. L. & Motter, A. E., Realistic control of network dynamics. Nat.Commun. 4, 1942 (2013). 
• Isidori, A., Nonlinear control systems (Springer Science & Business Media, 2013). 
• Haynes, G. & Hermes, H. Nonlinear controllability via lie theory. SIAM J. Control 8, 450–460 (1970). 
• Hermann, R. & Krener, A. Nonlinear controllability and observability. IEEE Trans. Automat.Contr. 22, 728–740 (1977). 
• Kailath, T. (1980). Linear systems (pp. 1–704). Prentice-Hall. 
• Kalman, R. E. (1968). Lectures on controllability and observability. Seminar on Controllability and Observability, Fondazione Guglielmo Marconi, Pontecchio Marconi, 1968. 
• Liu, Y.-Y., & Barabási, A.-L. (2016). Control principles of complex systems. Reviews of Modern Physics, 88(3), 247–58. http://doi.org/10.1103/RevModPhys.88.035006 
• Luenberger, D. G. (1979). Introduction to Dynamic Systems (pp. 1–231). John Wiley & Sons. 
• Lynn, C. W., & Basset, D. S. (2018). The physics of brain network structure, function, and control. arXiv.V, 1–75. 
• Pearl, J, Glymour, M. and Jewell, N.P., (2016). Causal inference in statistics: a primer, Wiley 
• Polderman, W. J., & Willems, J. (1998). Introduction to the mathematical theory of systems and control: a behavioural approach (pp. 1–458). Springer-Verlag. 
• Willems, J, The Behavioral Approach to Open and Interconnected Systems. (2007) IEEE Control Systems, 27(6), 46–99. http://doi.org/10.1109/MCS.2007.906923 
• Sontag, E. D. (1998). Mathematical Control theory: deterministic finite dimensional systems (pp. 1–544). Springer-Verlag. 
• Strogatz, S. (1994). Nonlinear dynamics and chaos (pp. 1–505). Readin, Massachusetts: Perseus books. 
• Sussmann, H. J. & Jurdjevic, V., Controllability of nonlinear systems. Differ. Equ. 12, 95–116 (1972). 
• Whalen, A. J., Brennan, S. N., Sauer, T. D. & Schiff, S. J. Observability and controllability of nonlinear networks: The role of symmetry. Phys. Rev. X 5, 011005 (2015). 
• Yamada, T., and L. R. Foulds, 1990, A graph‐theoretic approach to investigate structural and qualitative properties of systems: A survey, Networks 20, 427.

Peter Germann's open book on preferential flow

Peter German (GS) first raised the issue of how preferential flow in soils due to preferential flow in a famous paper with Keith Beven (GS) in 1982, Macropores flow in soils. A benchmark paper from which uncountable studies followed. Now retired, he wrote a book entitled "Preferential flow: Stokes approach to infiltration and drainage".

Since 1982 there was a great debate on preferential flow modelling which is not yet concluded. Germann's book is evidently  a contribution from a protagonist of this story and he had the kindness to make it open. I am not sure about the content. Stokesian flows are those that happens when all acceleration is dissipated, so the subtitle is not very informative on the content. More detailed comments will arrive when I will have read it. For now you can get it by clicking on the Figure.

Kirchner 2016 model

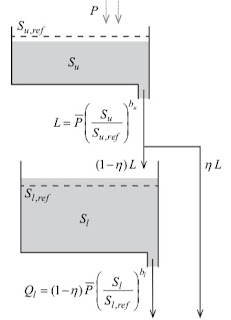
I open a new series of posts that analyze simple (or less simple) lumped (reservoir based) Hydrological Models. They are Dynamical Systems and they are well represented through Petri Nets introduced in Reservoirology #3. The present is the case of a simple two reservoirs model presented in Kirchner 2016 (from now on, K2016b).

Because of  its simplicity, K2016b is a nice case study to test and verify various aspect treated more abstractly in Rigon et al., 2016.  The presentation that contains K2016 is here.

Reference

Kirchner, J. W. (2016). Aggregation in environmental systems-Part 2. Catchment mean transit times and young water fractions under hydrologic non-stationarity. Hess, 20, 299–328. http://doi.org/10.5194/hess-20-299-2016

Richard Rotunno on the predictability of Storms

In these days we have here in Trento,  at my Department, Richard Rotunno (GS), a pleasant person and an outstanding scientist. His field of interest is meteorology and micrometeorology and, in particular, the evolution of storms.  Here in Trento he gave various seminars and in particular one  on the predictability of storms, which he permitted to share with you.

As usual, by clicking on the above image, you will be able to access the presentation. He cited some interesting papers that you will find below. On the butterfly effect, you can also see this my previous post, to which I think the literature cited by Richards add something important.

References (In the order in which they are cited)

• Charney, J.G; Fjörtoft, R and von Neumann, Numerical integration of the barotropic vorticity equation, Tellus, 2:4, 237-254, DOI: 10.3402/tellusa.v2i4.8607, 1950 
• Lynch, P., The origins of computer weather prediction and climate modeling” , J Comp Phys, doi:10.1016/j.jcp.2007.02.034, 2008 
• Thompson, P.D., “Uncertainty of Initial State as a Factor in the Predictability of Large Scale Atmospheric Flow Patterns”, Tellus IX, 1957 
• Lorenz, E.N., “The Predictability of a Flow which Possesses Many Scales of Motion” E. N. Lorenz, Tellus XX1, 1969 
• Palmer, T.N; Döring, A.; Seregin, G. The Real Butterfly Effect”. 27,9, R123, Nonlinearity 2014 
• Lilly, D.K., “Numerical Simulation Studies of Two-Dimensional Turbulence: II. Stability and Predictability Studies” Geophysical Fluid Dynamics, 4(1), 1972 
• Tennekes, H, Turbulent flow in two and three dimensions, Bull. Amer. Met. Soc., 59(1), 1978 
• Skamarock, W.C., Evaluating Mesoscale NWP Models Using Kinetic Energy Spectra, Monthly Weather Review, 2004 
• Patton, E.g. and Sullivan, P.P, Atmospheric stability influences on coupled boundary-layer-canopy turbulence, Journal of Atmos. Sci., https://doi.org/10.1175/JAS-D-15-0068.1, 2016 
• Falko, J., Insights into Atmospheric Predictability through Global Convection-Permitting Model Simulations, Journal of Atmos. Sci., https://doi.org/10.1175/JAS-D-17-0343.1, 2018

Floods in Alberto Viglione research

I had the honour to be in the committee that selected Alberto Viglione (GS) to become Associate Professor at Politecnico di Torino.  Alberto gave a nice seminar entitled "understanding and Estimating River Flood Hazards across Timescales" which covers some issues on flooding forecasting and variability in space-time.

I really appreciate his point of view which is different from mine and from which I can learn a lot, therefore I  asked him the permission to publish his presentation in my blog here. Please by clicking on the Figure above, find Alberto's presentation.

References

Archfield, S. A., R. M. Hirsch, A. Viglione, and G. Blöschl (2016), Fragmented patterns of flood change across the United States, Geophysical Research Letters, doi:10.1002/2016GL070590.

Barendrecht, M.H., A. Viglione and G. Blöschl (2017) A dynamic framework for
flood risk, Water Security, 1, 3-11, doi:10.1016/j.wasec.2017.02.001.

Blöschl, G., M. Sivapalan, T. Wagener, A. Viglione, and H. H. Savenije (2013b), Runoff Prediction in Ungauged Basins - Synthesis across Processes, Places and Scales, 484 pp., Cambridge University Press, ISBN:9781107028180.

Blöschl, G., et al. (2017), Changing climate shifts timing of European
floods, Science, 357 (6351), 588–590, doi:10.1126/science.aan2506.

Di Baldassarre, G., A. Viglione, G. Carr, L. Kuil, J. L. Salinas, and G. Blöschl (2013), Socio-hydrology: conceptualising
human-flood interactions, Hydrology and Earth System Sciences, 17, 3295–3303, doi:10.5194/hess-17-3295-2013.

Merz, R., and G. Blöschl (2008), Flood frequency hydrology: 1. Temporal, spatial, and causal expansion of information, Water Resources Research, 44, W08432, doi:10.1029/2007WR006744.

Salinas, J. L., A. Kiss, A. Viglione, R. Viertl, and G. Blöschl (2016), A fuzzy Bayesian approach to
flood frequency estimation with imprecise historical information, Water Resources Research, 52 (9), 6730–6750, doi:10.1002/2016WR019177.

Viglione, A., R. Merz, and G. Blöschl (2009), On the role of the runoff coefficient in the mapping of rainfall to flood  return periods, Hydrology and Earth System Sciences, 13 (5), 577–593, doi:10.5194/hess-13-577-2009.

Viglione, A., G. B. Chirico, R. A. Woods, and G. Blöschl (2010a), Generalised synthesis of space-time variability in flood response: An analytical framework, Journal of Hydrology, 394, 198–212, doi:10.1016/j.jhydrol.2010.05.047.

Viglione, A., G. B. Chirico, J. Komma, R. A. Woods, M. Borga, and G. Blöschl (2010b), Quantifying space-time dynamics of flood event types, Journal of Hydrology, 394, 213–229, doi:10.1016/j.jhydrol.2010.05.041.

Viglione, A., R. Merz, J. L. Salinas, and G. Blöschl (2013), Flood frequency hydrology: 3. A Bayesian analysis, Water Resources Research, 49 (2), 675–692, doi:10.1029/2011WR010782.

Viglione, A., G. D. Baldassarre, L. Brandimarte, L. Kuil, G. Carr, J. L. Salinas, A. Scolobig, and G. Blöschl (2014), Insights from socio-hydrology modelling on dealing with flood risk – Roles of collective memory, risk-taking attitude and trust, Journal of Hydrology, 518 (A), 71–82, doi:10.1016/j.jhydrol.2014.01.018.

Viglione, A. and M. Rogger (2015) Flood processes and hazards, Chapter 1.1 in: J.F. Schroder, P. Paron and G. Di Baldassarre (Eds.) HydroMeteorological Hazards and Disasters, Elsevier, pp. 3-33, doi:10.1016/
B978-0-12-394846-5.00001-1.

Viglione, A., B. Merz, N. V. Dung, J. Parajka, T. Nester, and G. Blöschl (2016), Attribution of regional flood changes based on scaling fingerprints, Water Resources Research, 52 (7), 5322–5340, doi:10.1002/2016WR019036