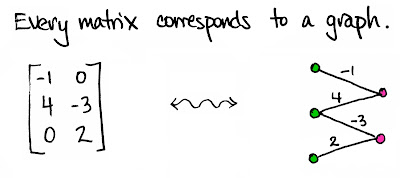How beatiful is this stuff on matrixes and graphs ?

Yes I know that graphs are represented by incidence and adiacency matrixes. However I never realize how a matrix can be represented by bipartite (or multipartite graphs). My attention was brought to it by the Math3ma blog (by Tai Danae Bradley) which I follow with delight (I am not saying that I am understanding all I read there). In particular this blog post entitles "Viewing matrices and probability as graphs".

The figure above comes from that blog and explain the concept that a matrix can be represented by a bipartite graph. If you understand it, then you can click on the Figure and continue your reading at the original blog.
After that, I noticed that the matrix representation is actually quite concise. Is it the minimal (using less numbers, excluding indexes) representation of the graph ? And, viceversa, given a graph, can we partitions its nodes in  sets such that any node in a group is connected with nodes in the other groups, but not with those in the same group ? If we are able to do so, we can subsequently build the matrix representation of the graph, reverting the process used in figure. If our set of nodes in the graph is tripartite, then the resulting matrix will be three-dimensional and so on.

In 1D (on the line) the partition is obvious and  is a bi-partition.  In 2D, the problem seems to be necessary a qudri-partition, at least for those graphs that are grids (cw-complexes): in fact the problem is the same of that brought to the four color problem. What happens in 3D ?

P.S. - Recently (2019-07-16)I found this interesting paper.

Quantify biological complexity - by John Baez

Just verbatim form the Azimuth blog (here). I place it also here for not forgetting it. Maybe later I will also comment it.

"Here’s a video of the talk I gave at the Stanford Complexity Group:


You can see slides here:

• Biology as information dynamics.

Abstract. If biology is the study of self-replicating entities, and we want to understand the role of information, it makes sense to see how information theory is connected to the ‘replicator equation’ — a simple model of population dynamics for self-replicating entities. The relevant concept of information turns out to be the information of one probability distribution relative to another, also known as the Kullback–Liebler divergence. Using this we can get a new outlook on free energy, see evolution as a learning process, and give a clearer, more general formulation of Fisher’s fundamental theorem of natural selection.

I’d given a version of this talk earlier this year at a workshop on Quantifying biological complexity, but I’m glad this second try got videotaped and not the first, because I was a lot happier about my talk this time. And as you’ll see at the end, there were a lot of interesting questions. "