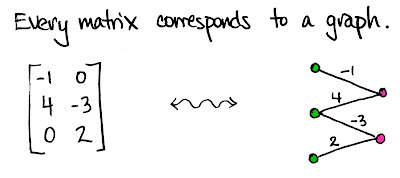Freeze and Cherry, 1979

Freeze and Cherry 1979 is a classical textbook on groundwater. Now it is available from the Hydrogeologists without borders site with permission from the Publisher.

Clicking on the image above, you are immediately redirected to their site.

Snow for GEOtop 4.0

We are going to  change GEOtop snow, we are struggling with the change since three years but beginning is always difficult. Today we are presenting some of the road we did and are goig to take.  At the fifth intercomparison meeting on SWE (modelling, measurements, remote sensing).

Get the presentation by clicking on the Figure above. The title is in Italian (Elements for the development of a new snow model for GEOtop 4.0), but the contents in English.
On similar topic were also the seminar by

• Giacomo Bertoldi, Entitled: Snow, Forest and Climate Change: which feedbacks ?

How beatiful is this stuff on matrixes and graphs ?

Yes I know that graphs are represented by incidence and adiacency matrixes. However I never realize how a matrix can be represented by bipartite (or multipartite graphs). My attention was brought to it by the Math3ma blog (by Tai Danae Bradley) which I follow with delight (I am not saying that I am understanding all I read there). In particular this blog post entitles "Viewing matrices and probability as graphs".

The figure above comes from that blog and explain the concept that a matrix can be represented by a bipartite graph. If you understand it, then you can click on the Figure and continue your reading at the original blog.
After that, I noticed that the matrix representation is actually quite concise. Is it the minimal (using less numbers, excluding indexes) representation of the graph ? And, viceversa, given a graph, can we partitions its nodes in  sets such that any node in a group is connected with nodes in the other groups, but not with those in the same group ? If we are able to do so, we can subsequently build the matrix representation of the graph, reverting the process used in figure. If our set of nodes in the graph is tripartite, then the resulting matrix will be three-dimensional and so on.

In 1D (on the line) the partition is obvious and  is a bi-partition.  In 2D, the problem seems to be necessary a qudri-partition, at least for those graphs that are grids (cw-complexes): in fact the problem is the same of that brought to the four color problem. What happens in 3D ?

P.S. - Recently (2019-07-16)I found this interesting paper.

If you want to study the Critical Zone of hillslopes, start from here

Recently a paper by Fan et al,  Hillslope Hydrology in Global Change Research and Earth System Modeling,  was published on  Water Resources Research, 85(3), 319–36. At the beginning I was thinking: "Hey, here it is another of those review papers which do not add anyhing to the existing literature".  This is not actually the case. The paper  is a very good introduction to many issues related to the Critical zone and its modelling and a source of relevant literature, of which I give an excerpt below.  The paper is open access and therefore you do not need any subscription to get it.

References

• Ajami, H., Khan, U., Tuteja, N., & Sharma, A. (2016). Development of a computationally efficient semi-distributed hydrologic modeling application for soil moisture, lateral flow and runoff simulation. Environmental Modelling and Software, 85(C), 319–331. http://doi.org/10.1016/j.envsoft.2016.09.002
• Anne Dudek Ronan, D. E. P. C. E. T. J. C. (2007). Field study and simulation of diurnal temperature effects on infiltration and variably saturated flow beneath an ephemeral stream, 1–17.
• Brantley, S. L., Lebedeva, M. I., Balashow, V. N., Singha, K., Sullivan, P. L., & Stinchcomb, G. (2017). Toward a conceptual model relating chemical reaction fronts to water flow paths in hills. Geomorphology, 277, 100–117. http://doi.org/10.1016/j.geomorph.2016.09.027
• Bui, O., Leoncini, X., Hal. (2019). Growth of a tree with allocations rules: Part 1 - Kinematics, 1–12.
• Chaney, N. W., van Huijgevoort, M. H. J., Shevliakova, E., Malyshev, S., Milly, P. C. D., Gauthier, P. P. G., & Sulman, B. N. (2018). Harnessing big data to rethink land heterogeneity in Earth system models. Hydrology and Earth System Sciences, 22(6), 3311–3330. http://doi.org/10.5194/hess-22-3311-2018
• Clark, M. P., Fan, Y., Lawrence, D. M., Adam, J. C., Bolster, D., Gochis, D. J., et al. (2015). Improving the representation of hydrologic processes in Earth System Models. Water Resources Research, 51(8), 5929–5956. http://doi.org/10.1002/2015WR017096
• Dearborn, K. D., & Danby, R. K. (2017). Aspect and slope influence plant community composition more than elevation across forest–tundra ecotones in subarctic Canada. Journal of Vegetation Science, 595–604. http://doi.org/10.1111/jvs.12521
• Elliot, P. E., & Cowell, C. M. (2015). Slope Aspect Mediates Fine Scale Tree Establishment Patterns at Upper Treeline during Wet and Dry Periods of the 20th Century. Artic, Antartic and Alpine Research, 1–13. http://doi.org/10.1657/AAAR0014-025
• Fan, Y., Clark, M., Lawrence, D. M., Swenson, S., Band, L. E., Brantley, S. L., et al. (2019). Hillslope Hydrology in Global Change Research and Earth System Modeling. Water Resources Research, 85(3), 319–36. http://doi.org/10.1029/2018WR023903
• Fan, Y., Miguez-Macho, G., Jobbagy, E. G., Jackson, R. B., & Otero-Casal, C. (2017). Hydrologic regulation of plant rooting depth. Pnas, 1–7. http://doi.org/10.1073/pnas.1712381114
• Fisher, R. A., Koven, C. D., Andreregg, W. R. L., Christoffersen, B. O., Dietze, M. C., Farrior, C., et al. (2017). Vegetation Demographics in Earth System Models: a review of progress and priorities. Global Change Biology, 1–74. http://doi.org/10.1111/ijlh.12426
• Hazenberg, P., Fang, Y., Broxton, P., Gochis, D., Niu, G. Y., Pelletier, J. D., et al. (2015). A hybrid-3D hillslope hydrological model for use in Earth system models. Water Resources Research, 51(10), 8218–8239. http://doi.org/10.1002/2014WR016842
• Hengl, T., Mendes de Jesus, J., Heuvelink, G. B. M., Ruiperez Gonzalez, M., Kilibarda, M., Blagotić, A., et al. (2017). SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE, 12(2), e0169748–40. http://doi.org/10.1371/journal.pone.0169748
• Krakauer, N. Y., Li, H., & Fan, Y. (2014). Groundwater flow across spatial scales: importance for climate modeling. Environ. Res. Lett., 9(3), 034003–8. http://doi.org/10.1088/1748-9326/9/3/034003
• Noe, S. M., & Giersch, C. (2004). A simple dynamic model of photosynthesis in oak leaves: coupling leaf conductance and photosynthetic carbon fixation by a variable intracellular CO2 pool. Functional Plant Biology, 31(12), 1195–19. http://doi.org/10.1071/FP03251
• Pelletier, J. D., Barron-Gafford, G., Gutierrez-Jurado, H., Hinckley, E. S., Istanbullioglu, E., McGuire, L. A., et al. (2017). Which way do you lean? Using slope aspect variations to understand Critical Zone processes and feedbacks 
• Earth Surface Processes and Landforms, 1133–1154. http://doi.org/10.1002/esp.4306
• Rempe, D. M., & Dietrich, W. E. (2018). Direct observations of rock moisture, a hidden component of the hydrologic cycle. Proceedings of the National Academy of Sciences, 115(11), 2664–2669. http://doi.org/10.1073/pnas.1800141115
• Riebe, C. S., Hahm, W. J., & Brantley, S. L. (2017). ESD Reviews: Thermodynamic optimality in Earth sciences. The missing constraints in modeling Earth system dynamics? Earth Surface Processes and Landforms, 42, 128–156. http://doi.org/10.1002/esp.4052
• Schaller, M. F., & Fan, Y. (2009). River basins as groundwater exporters and importers: Implications for water cycle and climate modeling. Journal of Geophysical Research, 114(D4), D07103–21. http://doi.org/10.1029/2008JD010636
• Sullivan, P. L., Price, R. M., Ross, M. S., Stoffella, S. L., Sah, J. P., Scinto, L. J., et al. (2016). Trees: a powerful geomorphic agent governing the landscape evolution of a subtropical wetland. Biogeochemistry, 128(3), 369–384. http://doi.org/10.1007/s10533-016-0213-9
• Tesfa, T. K., Tarboton, D. G., Chandler, D. G., & McNamara, J. P. (2009). Modeling soil depth from topographic and land cover attributes. Water Resources Research, 45(10), 103–17. http://doi.org/10.1029/2008WR007474
• Westhoff, M., Kleidon, A., Schymanski, S., Dewals, B., Nijisse, F., Renner, M., et al. (2019). ESD Reviews: Thermodynamic optimality in Earth sciences. The missing constraints in modeling Earth system dynamics? 
• , 1–31. http://doi.org/10.5194/esd-2019-6
• Winter, T. C., Harvey, J. W., Franke, O. L., & Alley, W. M. (1998). Ground Water and Surface Water. U.S. Geological Survey Circular (Vol. 1139, pp. 1–87).
• Worthington, S. R. H., Davies, G. J., & E, C. A. (2016). Enhancement of bedrock permeability by weathering. Earth-Science Reviews, 160, 1–73. http://doi.org/10.1016/j.earscirev.2016.07.002
• Xu, X., & Liu, W. (2017). The global distribution of Earth's critical zone and its controlling factors. Geophysical Research Letters, 44(7), 3201–3208. http://doi.org/10.1002/2017GL072760
• Yamazaki, D., Ikeshima, D., Tawatari, R., Yamaguchi, T., O'Loughlin, F., Neal, J. C., et al. (2017). A high-accuracy map of global terrain elevations. Geophysical Research Letters, 44(11), 5844–5853. http://doi.org/10.1002/2017GL072874