Yes I know that graphs are represented by incidence and adiacency matrixes. However I never realize how a matrix can be represented by bipartite (or multipartite graphs). My attention was brought to it by the Math3ma blog (by Tai Danae Bradley) which I follow with delight (I am not saying that I am understanding all I read there). In particular this blog post entitles "Viewing matrices and probability as graphs".
After that, I noticed that the matrix representation is actually quite concise. Is it the minimal (using less numbers, excluding indexes) representation of the graph ? And, viceversa, given a graph, can we partitions its nodes in sets such that any node in a group is connected with nodes in the other groups, but not with those in the same group ? If we are able to do so, we can subsequently build the matrix representation of the graph, reverting the process used in figure. If our set of nodes in the graph is tripartite, then the resulting matrix will be three-dimensional and so on.
In 1D (on the line) the partition is obvious and is a bi-partition. In 2D, the problem seems to be necessary a qudri-partition, at least for those graphs that are grids (cw-complexes): in fact the problem is the same of that brought to the four color problem. What happens in 3D ?
P.S. - Recently (2019-07-16)I found this interesting paper.
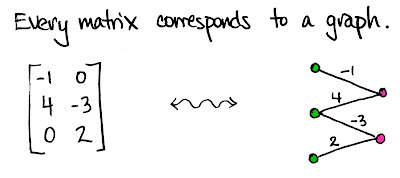
No comments:
Post a Comment