Ph.D. Miscellanea - Jupyter Notebook with R or Python on Statistics and Hydrology

This blog post is to share some of the notebooks provided by my Ph.D. students on the topics they follow in their Ph.D. classes. Please observe that some of the material are lecture notes by some of my colleagues. You can use them but you should cite the source when you do it.

• GEOstatistics (course held by Alberto Bellin)
• Statistics (course held by Stefano Siboni)

Data over Space and Time course by Cosma Shalizi

I confess I am a fan of Cosma Shalizi (GS). I do not know him, I do not know if he is a nice person or bad ass. He dos not know me. For sure I like the way he approaches statistics and his book (under the previous link). I am also astonished by his blog and the flood and variety of his readings.  Now he is giving a class on Spatial and temporal statistic. Topics that I think are necessary to know by Hydrologists. His class can be found here.

I hope that he does not mind if I cross reference his material.

Do not do statistics if you do not have casual effects in mind

Statistics was believed after the master of the last century to be the science of correlation, not of causation. However it is clear to our contemporary researchers, at least some of them, that interpreting data without any guess about causation can bring to wrong conclusion. Here below, please find an example from: "The book of why: the new science of cause and effect" by Judea Pearl and Dana MacKenzie.

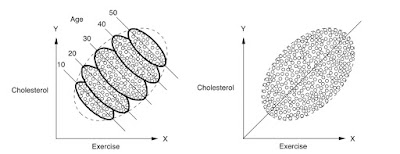
You should first look at the right figure. The scatterplot presents a roughly linear relation between Exercise and Cholesterol in blood. First observation, set this way, we probably have to reverse the axes. In a causal interpretation, it appears that exercise cannot cause cholesterol. On the contrary the cholesterol presence impose to the subjects to exercise more. Or there is something strange in data. More exercise cannot cause, by our normal belief, more cholesterol.
However, this is not actually even the main point. What the right figure suggests is that there is a positive correlation between the two variables: more cholesterol implies more exercise. However, as the left figure reveals, the real situation is not quite true. Because a cause of cholesterol is age, it appears that is reasonable to consider also this variable in the analysis. Then, when we separate the data among ages sets, we can see a further structure in the data and, in each class of age, in fact, the correlation between exercise and cholesterol is reversed. The less you exercise, the higher is your cholesterol. At the same time, the younger you are the less cholesterol you are expected to have in your blood. Now the picture is coherent with our causal expectations. I think there is something to learn. For more technical reader, one can give a look to: Casual Inference in Statistics.

Probability and Statistics basics: a very short simple overview of concepts for my students

These lectures cover both the class of Hydrology and Hydraulic Constructions that share the necessity to talk a little of statistics. In four steps I talk about simple concepts about statistics and probability. Very basic stuff to remind to my students what they should already know. Probably in the second series of slides I performed better.

Samples, Population, empirical distributions

Same topic as above but different class

Introduction to visual statistics, location and scale parameters.

Same topic as above but different class

Probability axioms and some derived concepts  visualised

Same topic as above, different class

Acting with Real numbers

Almost the same as above bur with a couple of slides more

Random sampling (is it defined in probability theory ?)

Really random numbers are not easily obtainable (if they exists). The short story: I perceive that in probability theory the concept of random sampling is not contemplated. Randomness is used by probability theory but is not implied by its axioms.

Randomly literally means that there is no law (expressed in equations) or algorithm (expressed in actions or some programing code) that connects one pick in the sequence to another.  The elements in the sequence can depend on others (as described by their correlation) while this dependence does not imply causation (in the sense that one implies the other): "correlation does not imply causation".
Taking the problem from a different perspective, Judea Pearl stresses that probability is about  "association'' not "causality'' (which is, in a sense, the reverse of randomness): "An associational concept is any relationship that can be defined in terms of a joint distribution of observed variables, and a causal concept is any relationship that cannot be defined from the distribution alone. Examples of associational concepts are: correlation, regression, dependence, conditional independence, like-lihood, collapsibility, propensity score, risk ratio, odds ratio, marginalization, conditionalization, ``controlling for,'' and so on.
Examples of causal concepts are:randomization, influence, effect, confounding, "holding constant,'' disturbance, spurious correlation, faithfulness/stability, instrumental variables, intervention, explanation, attribution, and so on. The former can, while the latter cannot be defined in term of distribution functions." He also writes: "Every claim invoking causal concepts must rely onsome premises that invoke such concepts; it cannot be inferred from, or even defined in terms statistical associations alone.''
Therefore Pearl, at least, in the sense that random elements in a random sequence are not causally related, supports the idea that if probability is not about causality, it is not either about ranmdomness.

Wikipedia also supports my arguments: "Axiomatic probability theory deliberately avoids a definition of a random sequence [2]. Traditional probability theory does not state if a specific sequence is random, but generally proceeds to discuss the properties of random variables and stochastic sequences assuming some definition of randomness. The Bourbaki school considered the statement ``let us consider a random sequence" abuse of language [3] "
The same Wikipedia explains very clearly which is the state of art of randomness concept but, for a more interested reader, the educational review paper by Volchan [4], is certainly informative.

I report from Wikipedia the current state of art for the extractions of random sequences:
"Three basic paradigms for dealing with random sequences have now emerged [5]:

•   The frequency / measure-theoretic approach. This approach started with the work of Richard von Mises and Alonzo Church. In the 1960s Per Martin-Loef noticed that the sets coding such frequency-based stochastic properties are a special kind measure zero sets, and that a more general and smooth definition can be obtained by considering all effectively measure zero sets.
•   The complexity / compressibility approach. This paradigm was championed by A. N. Kolmogorov along with contributions Levin and Gregory Chaitin. For finite random sequences, Kolmogorov defined the ``randomness'' as the entropy, Kolmogorov complexity, of a string of length K of zeros and ones as the closeness of its entropy to K, i.e. if the complexity of the string is close to K it is very random and if the complexity is far below K, it is not so random.
•   The predictability approach. This paradigm was due Claus P. Schnorr and uses a slightly different definition of constructive martingales than martingales used in traditional probability theory. Schnorr showed how the existence of a selective betting strategy implied the existence of a selection rule for a biased sub-sequence. If one only requires a recursive martingale to succeed on a sequence instead of constructively succeeds on a sequence, then one gets the recursively randomness concepts. Yongge Wang that recursively randomness concept is different from Schnorr's randomness concepts. "

"In most cases, theorems relating the three paradigms (often equivalence) have been proven.
I do not pretend to have fully understood the previous statements. However, in summary, we have to grow quite complicate if we want to understand what randomness is.
Once clarified what it is, we can have the problem to assess what can be a random arrangement for an arbitrary set of objects, say  $\Omega$. Taking example of the algorithms used to get a given random sequence of  numbers from a give distribution, we can observe that probability itself can be used to infer the random sequence of a set from a random sequence in [0,1] by inverting the probability $P$.

Random sampling is significant when the set of the domain is subdivided into disjoint parts: a partition. Therefore:

Definition: Given a set (having the structure of a~\(\sigma\)-algebra)~\(\Omega\) let a partition of
~\(\Omega\), denoted as:
${\mathcal P }(\Omega):=\{ x | \cup_{x \in \mathcal P} x = \Omega\, {\rm{and}}\ \forall y,z \in \Omega,\, y\cap z = \emptyset \}$
Through probability \(P\) defined over ${\mathcal P} (\Omega)$ each element $x$ of the set is mapped into the closed interval [0,1] and it is guaranteed that $P[\cup_{x \in \mathcal P} x] = 1$

There is not necessarily an ordering in the partition of $\Omega$ but we can arbitrarily arrange the set and associate each of its element with a subset of [0,1] of Lesbesgue measure (a.k.a. length) corresponding to its probability. By using the arbitrary order  of the partition, we can at the same time build the (cumulative) probability. By arranging or re-arranging the numbers in [0,1], we thus imply (since $P$ is bijective) a re-arrangement of the set ${\mathcal P} (\Omega)$.

Definition: we call sequence of elements in ${\mathcal P} (\Omega)$, denoted as $\mathcal S$ a numerable set of elements in ${\mathcal P} (\Omega)$:
$${\mathcal S} := \{ x_1 \cdot \cdot \cdot\}$$
Definition: we call a sequence a random sequence~~if it ha no
description shorter that itself via a universal Turing machine (orequivalently we can adopt one of the other two definition proposed above
Theorem: A random sequence of integers, through inverting the probability P, defines a random sequence on the set ${\mathcal P} (\Omega)$.
The prof is trivial. If there is a law that connects elements in ${\mathcal P} (\Omega)$ then through the probability $P$ a describing law is obtained also for the random sequence in [0,1], which is, therefore no more random.

So randomness of any set on which is defined a probability can be derived by getting a random sequence in [0,1].

References

[1] - Pearl, J. (2009). Causal inference in statistics: An overview. Statistics Surveys, 30, 96--146.
http://doi.org/10.1214/09-SS057
[2] Inevitable Randomness in Discrete Mathematics by József Beck 2009 ISBN 0-8218-4756-2 page 44
[3] Algorithms: main ideas and applications by Vladimir Andreevich Uspenskiĭ, Alekseĭ, Lʹvovich Semenov 1993 Springer ISBN 0-7923-2210-X page 166
[4] Sergio B. Volchan, What is a random sequences, The American Mathematical Monthly, Vol. 109, 2002, pp. 46–63[5] R. Downey, Some Recent Progress in Algorithmic Randomness, in Mathematical foundations of computer science 2004: by Jiří Fiala, Václav Koubek 2004 ISBN 3-540-22823-3 page 44

Copulas

So finally, I was obliged to try to understand what Copulas are. Put it simply. They are functions that connect marginal distributions to their multivariate distribution. Sklar (1959) theorem shows that the copula exists and is unique for any pair. Restricting to bivariate distribution function for sake of simplicity, Sklar theorem establish that the joint cumulative distribution $H(x,y)$ of any pair of continuous random variable (X,Y) may be written as as:
$$
H(x,y) = C(F(x),G(y)) \ \ \ \forall x, y \in \mathbb{R}
$$
where $F(x)$ and $G(y)$ are the marginal distributions of $X$ and $Y$. $C$, the copula, can be though as a function such that:
$$
C:\, [0,1]^2 \mapsto [0,1]
$$

Obviosly just in the Platonic world where you know $H$,$F$ and $G$, you can determine the unknown $C$. In practice you work with much less information, where you have the marginals, $F$ and $G$ and, maybe some information about the correlation of the random variables they describe.
So you have to infer the multivariate distribution, by selecting, as usual I would say, the copulas among a large set of copulas templates.
This is what is written for instance in Genest and Favre 2007, a paper particularly directed to hydrologists. So, for your introduction to Copulas you can probably start from that paper. However, I came to it, by its citation in Ebrechts, 2009. Traditional references on the subject are the books by Joe (1997) and Nelsen (1999) but a nice review paper (therefore more synthetic) is Frees and Valdez 1998.
Particularly relevant copulas are useful to understand correlations among variables, and the so called empirical copulas (e.g. Genest and Favre, 2007) can be used to this scope.
Among Hydrological application, I can mention, among others, De Michele and Salvadori (2002), Salvadori and De Michele (2004), Grimaldi and Serinaldi (2006), and Serinaldi et al., 2009.

References

• De Michele, C. (2003). A Generalized Pareto intensity-duration model of storm rainfall exploiting 2-Copulas. Journal of Geophysical Research, 108(D2), 225–11. http://doi.org/10.1029/2002JD002534
• Embrechts, P. (2009). Copulas: a personal view, 1–18.
• Frees, E. W., & Valdez, E. A. (1999). Understanding Relationships Using Copulas. North American Actuarial Journal, 2(1), 1–25. 
• Genest, C., & Favre, A. A.-C. (2007). Everything you always wanted to know about copula modeling but were afraid to ask. Journal of Hydrologic Engineering, 347–368. http://doi.org/10.1061/ASCE1084-0699200712:4347
• Genest, C., & Nešlehová, J. (2007). A primer on copulad for count data. Astin Bulletin, 37(02), 475–515. http://doi.org/10.1017/S0515036100014963
• Grimaldi, S., & Serinaldi, F. (2006). Asymmetric copula in multivariate flood frequency analysis. Advances in Water Resources, 29(8), 1155–1167. http://doi.org/10.1016/j.advwatres.2005.09.005
• Joe, H. 1997 . Multivariate models and dependence concepts, Chapmanand Hall, London. 
• Mikosch, T. (2006). Copulas: Tales and facts. Extremes, 9(1), 3–20. http://doi.org/10.1007/s10687-006-0015-x
• Nelsen, R. B. 1999 . An introduction to copulas, Springer, New York. 
• Salvadori, G., & De Michele, C. (2004). Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resources Research, 40(12), 194–17. http://doi.org/10.1029/2004WR003133
• Serinaldi, F., Bonaccorso, B., Cancelliere, A., & Grimaldi, S. (2009). Probabilistic characterization of drought properties through copulas. Physics and Chemistry of the Earth, 34(10-12), 596–605. http://doi.org/10.1016/j.pce.2008.09.004

Jackknife

I found this nice paper on Jackknife, worth to read. Easy also to understand the differences between the jackknife technique and the leave-one-out one.

You can click on the knife to download it. 

Probabilità in pillole

Per imparare bene la teoria delle probabilità, non c'e' dubbio lo studio approfondito di qualche buon libro è necessario. Per una piccola bibliografia personale, si veda il post "Learn Statistics and Probability!" Ma per una ripasso in pillole, ecco quanto detto e fatto a lezione:

1 - Introduzione (Audio 2015: 6Mb. YouTube 2017)
2 - Assiomi (Audio 2015: 12.6 Mb)
3 - Domini discreti e Spazi metrici (Audio 2015: 11.3 Mb)
4 - Distribuzioni uniforme e gaussiana univariate (Audio 2015: 13.9 Mb)
5 - Distribuzioni univariate di interesse idrologico (Audio 2015: 7.9 Mb)
6 - Random sampling
7 - Il teorema del limite centrale e la legge dei grandi numeri (Audio 2015: 4.2 Mb)

Altre risorse:

Le slides tutte assieme: Un ripasso di probabilità.

Audio 2014:

I Assiomi, Bayes etc. - 22Mb;
II - Distribuzioni di Probabilità - 5.6 Mb).

Qui un sintetico manualetto con alcuni temi "non standard" (dovuto a Falcioni e Vulpiani).

Misura e rappresentazione dei dati idrologici

Ecco qui la presentazione sui dati idrologici, suddivisa in parti:

• La Misura. (Audio 2015: 5.5 Mb)
• Le caratteristiche dei dati idrologici (Audio 2015: 5 Mb)
• Serie temporali di dati idrologici (Audio 2015: 8.5Mb)
• Variabilità spaziale delle misure idrologiche (Audio 2015: 4.1Mb)
• Raccolta e archiviazione dei dati idrologici (Audio 2015: 6.5 Mb)

Tutto il blocco di argomentii assieme nella versione 2014. Audio (21.6 Mb)

Bibliografia

• Agnoli, P.,  Il senso della misura, la codifica della realtà tra filosofia, scienza ed  esistenza umana, Armando Editore, 2004            
• Agnoli, P., Breve introduzione storica alle prime unità di misura, http://www.roma1.infn.it/~dagos/SSIS/PaoloAgnoli_appuntimisure.pdf , 2006, last retrieved 2011/03/18
• AA.VV, Le misure nella scienza, nella tecnica, nella società, Manuale di metrologia,  a cura di S. Sartori,   Paravia, Torino,1979
• AA. VV,  Le misure di grandezze fisiche, a  cura di E. Arri e S. Sartori, Paravia, 
• Torino,1984 
• Burroughs, W., J, Weather Cycles,  Cambridge U. P.,  2003
• Grünewald, T., Schirmer, M., Mott, R., & Lehning, M. (2010). Spatial and temporal variability of snow depth and ablation rates in a small mountain catchment. The Cryosphere, 4(2), 215-225. doi:10.5194/tc-4-215-2010
• Loreti, M., Teoria degli Errori e Fondamenti di Statistica: Introduzione alla Fisica Sperimentale, 2006, http://wwwcdf.pd.infn.it/labo/INDEX.html, last retrieved 2011/03/18
• Roth, K. (2007). Soil Physics Lecture Notes (p. 1-340), 2007, http://www.iup.uni-heidelberg.de/institut/forschung/groups/ts/soil_physics/students/lecture_notes05/sp.pdf, last retrieved 2011/03/18
•  Shuttleworth, W. James (January/February 2008). "Evapotranspiration Measurement Methods". Southwest Hydrology (Tucson, AZ) 7 (1): 22–23. Retrieved 2009-07-22.
• Western, Andrew W. (2005). "Principles of Hydrological Measurements". In Anderson, Malcolm G.. Encyclopedia of Hydrological Sciences. 1. West Sussex, England: John Wiley & Sons Inc.. pp. 75–94
• Tabony, R. C.  (1979), A spectral filter analysis of long period records in England and Wales, Meterol. Mag. 108, 97-119 
• Zambrano-Bigiarini, M. (2010). On the effects of hydrological uncertainty in assessing the impacts of climate change on water resources, 1-293.

Links to web sites

• http://en.wikipedia.org/wiki/Outline_of_hydrology,  last retrieved 2011/03/18                             
• http://en.wikipedia.org/wiki/History_of_measurement, last retrieved 2011/03/18                            
• http://www.paoloagnoli.it/immagini/Tesi%20Filosofia%20P.%20Agnoli.pdf, last retrieved 2011/03/18                                                                                                                                         
• http://www.metrum.org/measures/index.htm, last retrieved 2011/03/18

Other types of numerics (for ecology)

When I think to numerics, I always think to the "Concrete Mathematics" that Donald Knuth taught to us, or to way to integrate partial differential equations. Recently, however, I came across the book by Legendre and Legendre called "Numerical Ecology", which is something different.

 The work is something in between statistics and classification or clustering stuff, interpretation of structures. Interpretation of spatial data. A hybrid of things, in my view, interesting to know, anyway.

Reference

Legendre, P and Legendre L, Numerical Ecology, Amsterdam, Elsevier, 2003

Machine Learning

I found this informative blog post on Element of Statistic Learning, a fundamental book by Trevor Hastie and Rob Tibshirani.

I reproduce verbatim the blogpost:

"In January 2014, Stanford University professors Trevor Hastie and Rob Tibshirani (authors of the legendaryElements of Statistical Learning textbook) taught an online course based on their newest textbook, An Introduction to Statistical Learning with Applications in R (ISLR). I found it to be an excellent course in statistical learning (also known as "machine learning"), largely due to the high quality of both the textbook and the video lectures. And as an R user, it was extremely helpful that they included R code to demonstrate most of the techniques described in the book.

If you are new to machine learning (and even if you are not an R user), I highly recommend reading ISLR from cover-to-cover to gain both a theoretical and practical understanding of many important methods for regression and classification. It is available as a free PDF download from the authors' website.

If you decide to attempt the exercises at the end of each chapter, there is a GitHub repository of solutions provided by students you can use to check your work.

As a supplement to the textbook, you may also want to watch the excellent course lecture videos(linked below), in which Dr. Hastie and Dr. Tibshirani discuss much of the material. In case you want to browse the lecture content, I've also linked to the PDF slides used in the videos.

Chapter 1: Introduction (slides, playlist)

• Opening Remarks and Examples (18:18)
• Supervised and Unsupervised Learning (12:12)

Chapter 2: Statistical Learning (slides, playlist)

• Statistical Learning and Regression (11:41)
• Curse of Dimensionality and Parametric Models (11:40)
• Assessing Model Accuracy and Bias-Variance Trade-off (10:04)
• Classification Problems and K-Nearest Neighbors (15:37)
• Lab: Introduction to R (14:12)

Chapter 3: Linear Regression (slides, playlist)

• Simple Linear Regression and Confidence Intervals (13:01)
• Hypothesis Testing (8:24)
• Multiple Linear Regression and Interpreting Regression Coefficients (15:38)
• Model Selection and Qualitative Predictors (14:51)
• Interactions and Nonlinearity (14:16)
• Lab: Linear Regression (22:10)

Chapter 4: Classification (slides, playlist)

• Introduction to Classification (10:25)
• Logistic Regression and Maximum Likelihood (9:07)
• Multivariate Logistic Regression and Confounding (9:53)
• Case-Control Sampling and Multiclass Logistic Regression (7:28)
• Linear Discriminant Analysis and Bayes Theorem (7:12)
• Univariate Linear Discriminant Analysis (7:37)
• Multivariate Linear Discriminant Analysis and ROC Curves (17:42)
• Quadratic Discriminant Analysis and Naive Bayes (10:07)
• Lab: Logistic Regression (10:14)
• Lab: Linear Discriminant Analysis (8:22)
• Lab: K-Nearest Neighbors (5:01)

Chapter 5: Resampling Methods (slides, playlist)

• Estimating Prediction Error and Validation Set Approach (14:01)
• K-fold Cross-Validation (13:33)
• Cross-Validation: The Right and Wrong Ways (10:07)
• The Bootstrap (11:29)
• More on the Bootstrap (14:35)
• Lab: Cross-Validation (11:21)
• Lab: The Bootstrap (7:40)

Chapter 6: Linear Model Selection and Regularization (slides, playlist)

• Linear Model Selection and Best Subset Selection (13:44)
• Forward Stepwise Selection (12:26)
• Backward Stepwise Selection (5:26)
• Estimating Test Error Using Mallow's Cp, AIC, BIC, Adjusted R-squared (14:06)
• Estimating Test Error Using Cross-Validation (8:43)
• Shrinkage Methods and Ridge Regression (12:37)
• The Lasso (15:21)
• Tuning Parameter Selection for Ridge Regression and Lasso (5:27)
• Dimension Reduction (4:45)
• Principal Components Regression and Partial Least Squares (15:48)
• Lab: Best Subset Selection (10:36)
• Lab: Forward Stepwise Selection and Model Selection Using Validation Set (10:32)
• Lab: Model Selection Using Cross-Validation (5:32)
• Lab: Ridge Regression and Lasso (16:34)

Chapter 7: Moving Beyond Linearity (slides, playlist)

• Polynomial Regression and Step Functions (14:59)
• Piecewise Polynomials and Splines (13:13)
• Smoothing Splines (10:10)
• Local Regression and Generalized Additive Models (10:45)
• Lab: Polynomials (21:11)
• Lab: Splines and Generalized Additive Models (12:15)

Chapter 8: Tree-Based Methods (slides, playlist)

• Decision Trees (14:37)
• Pruning a Decision Tree (11:45)
• Classification Trees and Comparison with Linear Models (11:00)
• Bootstrap Aggregation (Bagging) and Random Forests (13:45)
• Boosting and Variable Importance (12:03)
• Lab: Decision Trees (10:13)
• Lab: Random Forests and Boosting (15:35)

Chapter 9: Support Vector Machines (slides, playlist)

• Maximal Margin Classifier (11:35)
• Support Vector Classifier (8:04)
• Kernels and Support Vector Machines (15:04)
• Example and Comparison with Logistic Regression (14:47)
• Lab: Support Vector Machine for Classification (10:13)
• Lab: Nonlinear Support Vector Machine (7:54)

Chapter 10: Unsupervised Learning (slides, playlist)

• Unsupervised Learning and Principal Components Analysis (12:37)
• Exploring Principal Components Analysis and Proportion of Variance Explained (17:39)
• K-means Clustering (17:17)
• Hierarchical Clustering (14:45)
• Breast Cancer Example of Hierarchical Clustering (9:24)
• Lab: Principal Components Analysis (6:28)
• Lab: K-means Clustering (6:31)
• Lab: Hierarchical Clustering (6:33)

Interviews (playlist)

• Interview with John Chambers (10:20)
• Interview with Bradley Efron (12:08)
• Interview with Jerome Friedman (10:29)
• Interviews with statistics graduate students (7:44)"

New Course on statistics and data inference on Coursera

Verbatim from DataCamp Blog:

" Yesterday (Monday 1st of September), a new session of Data Analysis and Statistical Inference, taught by Doctor Mine Çetinkaya-Rundel from Duke university, has started on Coursera. Just like with the previous run, all labs take place in DataCamp’s interactive learning environment.

Data Analysis and Statistical Inference will teach you how to make use of data in the face of uncertainty. Throughout the course, you will learn how to collect, analyze, and use data to make inferences and conclusions about real world phenomena. No formal background is required, but mathematical skills are definitely a plus."

Further information here.

Cartoon guide to statistics

Since I am supporting the idea that Hydrologists should know very well statistics, it is with pleasure that I discovered in Rbloggers these two cartoon guides to statistics.

The first is the Cartoon guide to statistics by Gomick and Smith from which the figure above is an excerpt.

"Witty, pedagogical and comprehensive, this is the best book of the bunch! It provides a historical perspective and covers quite advanced topics such as confidence intervals, regression analysis and probability theory. The book contains a fair deal of mathematical notation but still manages to be accessible." MarkR

The second one is the Manga guide to statistics by Shin Takahashi and illustrated by Iroha Inoue.

"As opposed to the Cartoon Guide to Statistics the Manga Guide reads more like a standard comic book with panels and a story line. The story centers around the schoolgirl Rui who wants to learn statistics to impress the handsome Mr. Igarashi. To her rescue comes Mr. Yamamoto, a stats nerd with thick glasses. The story and the artwork is archetypal manga (including very stereotype gender roles) but if you can live with that it is a pretty fun story."MarkR

Again on statistics - P - Values

A Nature paper brings back arguments on what p-values are, and how they should be consider. It also talks about the different positions of Fisher, Neyman and Pearson, on the topic [please notice that the reconstruction of the history gives a little more information than the one I gave in my previous post citing J. Franklin], and I,  quite clearly, vote for Fisher. You can find the article here.

A lot of comments follow. However, the right complements of the Nature paper seems to this "LessWrong blopost" and this other on Prudentia.

Learn Statistics and Probability !

In one of my previous posts, I talked about the necessity to use (and therefore learn) statistics. As said in "What is Statistics?", anyone working with data is using statistics. This simplifies a lot the approach. Actually I arrived to statistics mostly from the teaching side. As a scientist, indeed, I often overlooked statistics.  Even if, in part of my research statistics appears, it would be a gross exaggeration to say that I approached it consciously (kind of take it for granted). Time to time I used (ripped off) methods to fit data, but I never had a systematical approach to it. 

From the teaching side, I had instead to communicate some concepts to students, and thus I tried to be more methodical. My efforts of synthesis  produced my slides on probability and on statistics. In fact I solved the dualism between the two by saying that statistics has to do with reality, while probability is an axiomatic theory, which leave out the identification of what the probability itself is (De Finetti teaches). What people usually do is to search for a "model" among the one available in the "models market" (and therefore there is a phase where these models are "invented" analysed theoretically). The models in turns are distribution functions, regression functions, or whatever function(al) is necessary. In a second phase, you have then to see how the model of your choice adapts (fits!) to real life. In this adaptation you rely on statistics and statistical methods and on Bayes theorem. You can interpret the procedure according to a frequentist approach or through a Bayesian one. The latter procedure is becoming dominant in the field I frequent, but probably has to escape some inductive traps (i.e. the idea that just from induction one can get knowledge, while the scientific method has a hypothetical-deductive structure: look at Bayes here). In fact, there could be a third approach, where "the machines" find the model for you (see Breiman,  2001 and discussions therein ^1).

While the concept of distribution remains always under the hood of any approach (maybe less evident in Machine Learning) and can probably used as a “connecting principle”, in my ignorant perception of the matter the whole picture remains a little obscure.

The fact is that the principles of statistics (and of probability) are taught abstractly thinking to a A -> [0,1] application where A is some undefined set, and, most of the time, when thinking to applications we are using some subspace of R^n, the real numbers, into [0,1], but the object of investigation is a single value of a single quantity (let say a unique measure - do not charge here the word of mathematical significance - of a quantity). Using the concepts of hydrology, this would cover a zero-dimensional domain or (modelling). 

In fact hydrology, and reality, are perceived as multidimensional. So important applications and important measures vary, for instance, in time.  This fact confuses your  ideas since in principle we have to analyse many quantities (as many as the instant of time)  so our application is not anymore, at the very general stage, the study of a single quantity but of many quantities. However,  either for practical or for physical reasons we often conceive these quantities as the manifestation of a sigle one (as the realisation of the same hidden probabilistic structure repeated many times, not necessarily with whatsoever relation between them). 

For good or for bad, this is usually ignored theoretically while, in practice, it brings to a separate subfield, of which time series analysis is an example.  Also fitting one variable versus another (or others) falls in the same dimensional domain. It appears in books smoothly, as it would be natural, but it always let me with some discomfort. Only in the statistical book by von Storch and Zwiers, my dimensional distinction appears (especially looking at the book's index). In classical books, this passage is actually mediated by looking at random-walks, Markov chains, martingales and other similar topics. The key of this passage of dimensionality is the introduction of some correlation -in the common language sense, but also in the probabilistic sense - that ties one datum to another (the subsequent one).

A further, and consequent, passage happens when one moves to analyse not a line of events but, a space of events, with the further complication that multiple dimensions cannot even exploit the ordering of 1-D problems. 

Nowadays patterns in two or multidimensional spaces, in fact, are discovered by machines (at least if I properly understand the concept of Machine Learning), with, again, some danger to fall in an excessive inductivism. 

Going to the point how to learn this stuff. I would start from a book on probability where the axiomatic structure of the field would be clear.  In my formation, this role was accomplished by the old classic, Feller’s (1968) book. (Let say the first two chapters, which are now reproduced in almost all the textbooks. Then the following chapter, but skipping the * sections. Possibly section XI concludes this first -0-D- part (Waiting times appears: but they are not actually related to “time” but to an “ensable” of trials). Looking for on-line resources, I also found the book by Grinstead that covers more or less the same topics. 

The probabilistic part should be complemented, at this point by some statistics. Most  of the good statistical books simply redo all probability theory from a more practical point of view, before going to their specific, how to infer from data their distribution (if any exists),  but these can be skipped or just browsed, then.  As J. Franklin says “Mathematicians, pure and applied, think there is something weirdly different about statistics. they are right. It is not part of combinatorics or measure theory, but an alien science with its own modes of thinking. Inference is essential to it, so it is, as Jaynes says, more a form of (non-deductive) logic.” 

Being prepared to controversies, a  couple of good books for learning statistics with climate and/or hydrologic orientation are the book by Hans von Storch and Francis W. Zwiers or Kottegoda and Rosso (expensive) books.  These have the advantage to  use hydro-meteorological datasets examples. In these, after the first chapters, the subsequent chapters follow a perspective where the goal is to  choose “a model, a distribution or process that is believed from tradition or intuition to be appropriate to the class of problems in question”, and subsequently “statistically validate” it using data to estimate the parameters of the model. “That picture, standardised by Fisher and Neyman in the 1930s, has proved in many ways  remarkably serviceable. It is especially reasonable where it is known that the data are generated by  a physical process that conforms to the model. As a gateway to these mysteries, the combinatorics of dice and coins are recommended; the energetic youth who invest  heavily in the calculation of relative frequencies will be inclined to protect their investment through faith in the frequentist philosophy that probabilities are all really relative frequencies.” (also from J. Franklin, 2005). 

My favorite reading on many of these statistical computing techniques  are the Cosma Shalizi’s notes which certainly presents the topics in an original way that cannot be found elsewhere. Shalizi’s  notes, as well as Gareth et al (2013)  ones have also the advantage to use R as computational tool, and to present some modern topic like a chapter on Machine Learning.  Hastie et al., 2005 is instead an advanced lecture on the same topics. These books are actually more decisely oriented to statistical modelling, as well as is the Hyndman and Athanasopoulos (2013) free (and simple) on line book (also using R). 

Kottegoda and Rosso book hosts also a chapter on Bayesian statistics, which is the other way to see statistical inference. A brief introduction to the Bayesian mistery is Edward Campbell’s brief technical report that can be found here. The possibly longest one, which present a different approach to probability, is the posthumous masterpiece by Jaynes (2003), which is probably a fundamental reading on the topic. 

However, my personal understanding of the Bayesian methodology gained some consistency only after the reading of G. D’Agostini (2003) book. Actually D’Agostini can be defined as a Bayesian evangelist, but its arguments, even if some examples in high particle physics remain to me actually unclear, convinced me to a mild conversion.

As a matter of fact, my real understanding of the Bayesian approach is still poor. Not because I did not understand the theory, but because between the theory and its application there is a gap which I still do not have filled. (Practice it!)

Looking at all of these contributions, sum up to thousands of pages. Possibly many of these pages are repetitions of the same concepts. Sometimes from slightly different point of view. To the reader the choice of what to do. 

A last note regards how to made calculations.  For doing it R is certainly a good choice, that some of the cited books’ authors already did, and the support for doing it really is large and growing.

Notes

^1 - The paper is also remarkable for sir David Cox (he also has his introductory and conceptual book) answer. Cox, besides being a prominent British statistician, has quite a carrier in hydrology, especially looking at his work on rainfall and eco-hydrology together with Ignacio Rodriguez-Iturbe.

References (with some additions to the text)

Berliner, L. M., & Royle, J. A. (1998). Bayesian Methods in the Atmospheric Sciences, 6, 1–17.

Breiman, L. (2001). Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Statistical Science, 16(3), 199–231. doi:10.1214/ss/1009213726

Campbell, E. P. (2004). An Introduction to Physical-Statistical ModellingUsing Bayesian Methods (pp. 1–18).

Cox, D. R., & Donnelly, C. A. (2011). Principles of applied statistics. Cambridge University Press.

D'Agostini, G. (2003). Bayesian_Reasoning_in_Data_Analysis__A_Critical_Introduction (I. pp. 1–351).World Scientific.

Durrett, R. (2010). Probability: theory and examples.

Feller, W. (1968). An Introduction to Probability Theory and Its Applications (pp. 1–525).

Feller, W. (2007). The fundamental limit theorems in Probability, 1–33.

Fienberg, S. E. (2014). What Is Statistics? Annual Review of Statistics and Its Application, 1(1), 1–9. doi:10.1146/annurev-statistics-022513-115703

Franklin, J. (2005). Probability Theory: The Logic of Science - The Fundamental of Risk Measurements - The Element of statistical learning - Review, 2, 1–5.

Gelman, A. (2003). A Bayesian Formulation of Exploratory Data Analysis and Goodness‐of‐fit Testing*. International Statistical Review. doi:10.1111/j.1751-5823.2003.tb00203.x

Grinstead, C. M. and Snell JL (2007). Introduction to Probability (pp. 1–520).

Guttorp, P. (2014). Statistics and Climate. Annual Review of Statistics and Its Application, 1(1), 87–101. doi:10.1146/annurev-statistics-022513-115648

James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning, 103. doi:10.1007/978-1-4614-7138-7

Jaynes, E. T. (2003). Probability theory: the logic of science.

Kharin, S. (2008c, May 19). Statistical concepts in climate research - I. slides

Kharin, S. (2008b, May 19). Classical Hypothesis Testing. -II slides

Kharin, S. (2008a). Climate Change Detection and Attribution: Bayesian view, 1–35. III slides

Kottegoda, N. T., & Rosso, R. (2008). APPLIED STATISTICS FOR CIVIL AND ENVIRONMENTAL ENGINEERS (pp. 1–737).

Madigan, D., Stang, P. E., Berlin, J. A., Schuemie, M., Overhage, J. M., Suchard, M. A., et al. (2013). A Systematic Statistical Approach to Evaluating Evidence from Observational Studies. Annual Review of Statistics and Its Application, 1(1), 131125173259005. doi:10.1146/annurev-statistics-022513-115645

Shalizi, C. R. (2014). Advanced Data Analysis from an Elementary Point of View (pp. 1–584).

Storch, von, H., & Zwiers, (2003) F. W. (n.d.). Statistical analysis in climate research. Cambridge University Press

Zwiers, F. W., & Storch, von, H. (2004). On the role of statistics in climate research. International Journal of Climatology, 24(6), 665–680. doi:10.1002/joc.1027

The law of small numbers

I did know the law of large numbers (and its violations) but I never reflected about the law of small numbers.

You can learn about following this link. It is mostly about Poisson distribution which is, indeed ubiquitous also in Hydrology. So the reading of this R-related post is certainly interesting and useful also for us.

91 video tutorial for learning R

You can find them at:

http://www.twotorials.com/

Enjoy!